Houdini-Fun
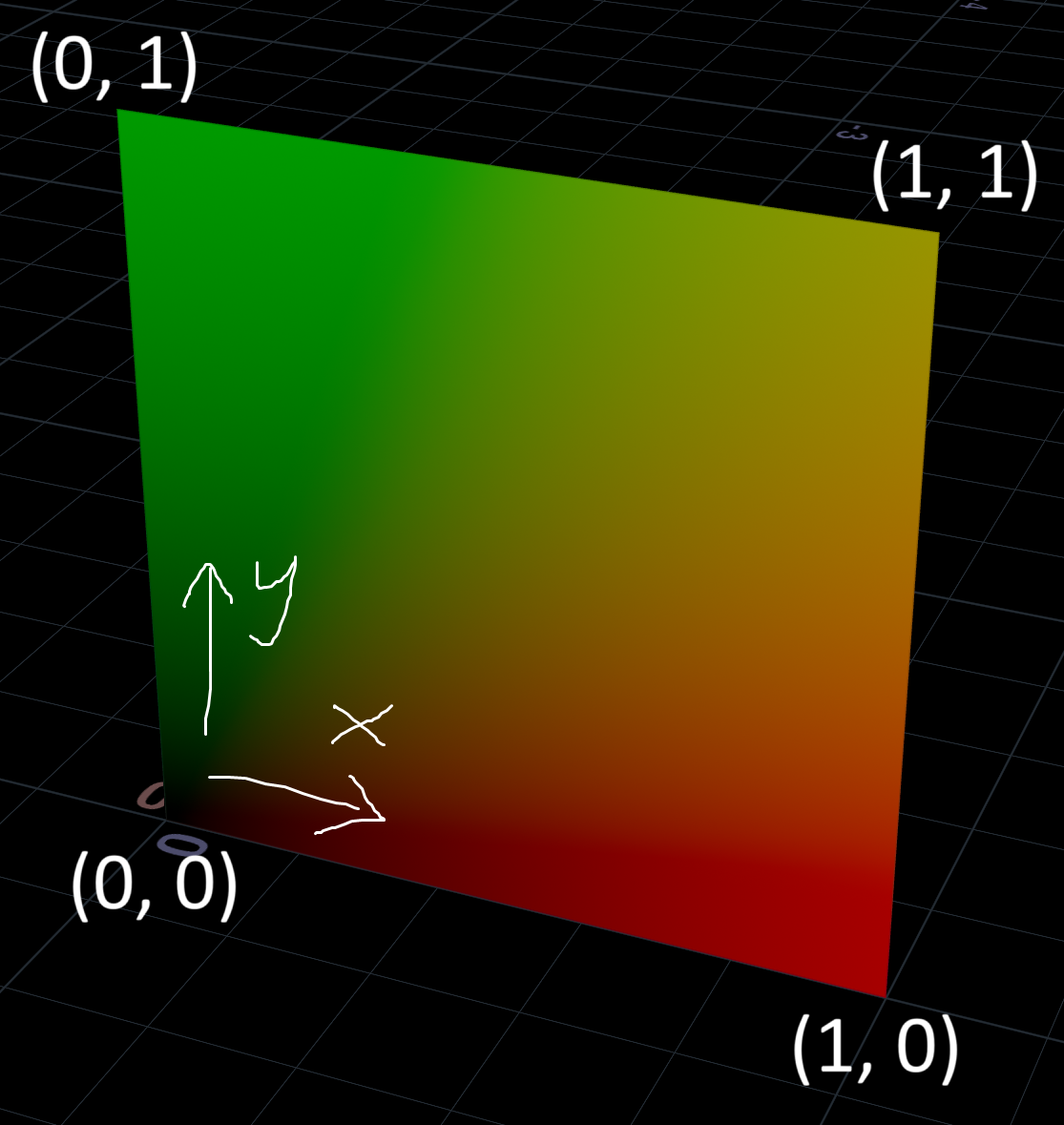
Houdini Normalized Device Coordinates
NDC is a screen space coordinate system, great for perspective illusions and raycasting tricks.
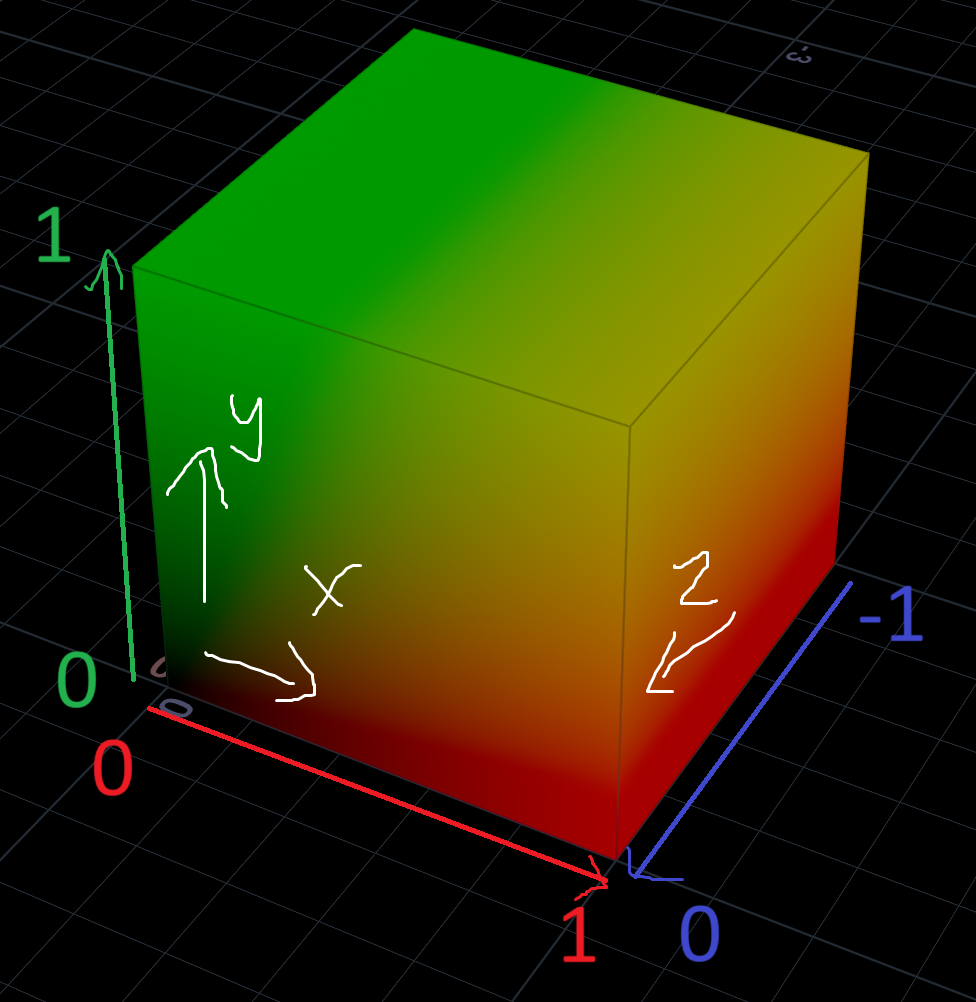
X and Y represent the 2D screen coordinates, while Z represents the distance to the camera.
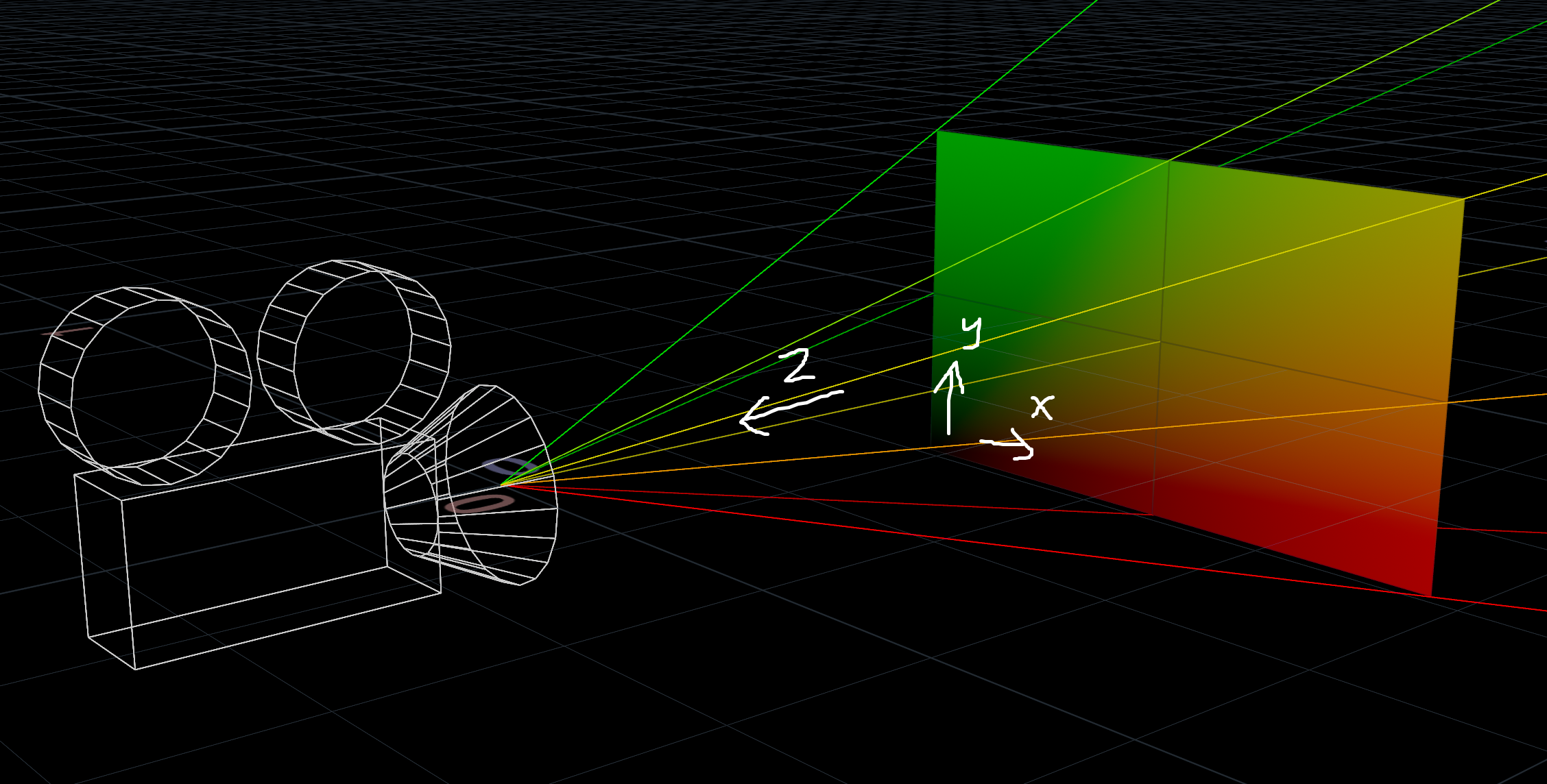
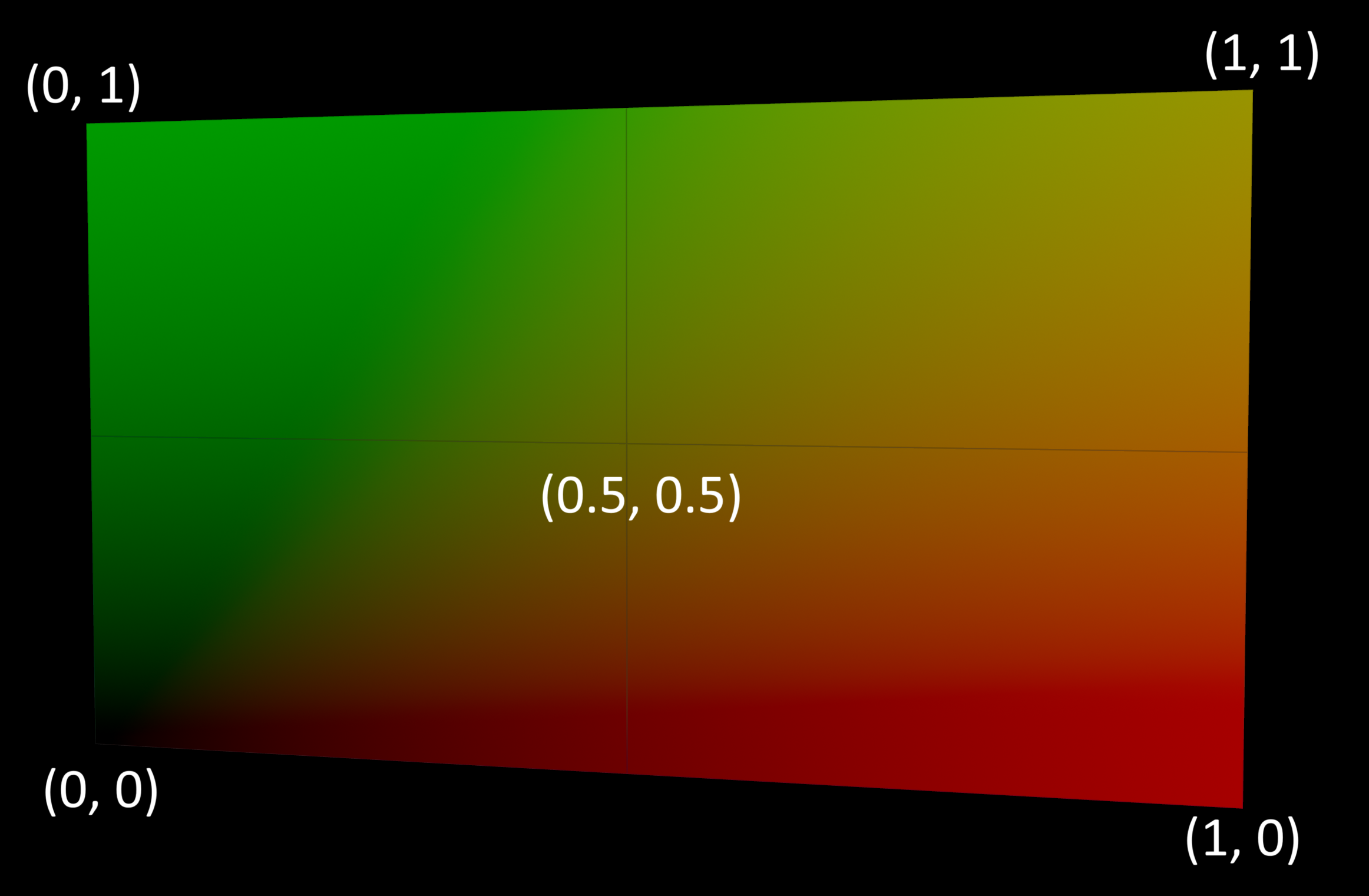
The X and Y coordinates are normalized between 0 and 1, with 0.5 in the middle.
The Z coordinates are 0 at the camera, negative in front and positive behind the camera. Why negative? No idea!

Converting NDC
You can convert a world space coordinate to NDC using toNDC():
vector ndcPos = toNDC(chsop("cam"), v@P);
Then convert it back to world space using fromNDC():
vector worldPos = fromNDC(chsop("cam"), ndcPos);
Here’s some NDC tricks you can play with.
| Download the HIP file! | | — |
Get the camera position
The origin of NDC space is the camera, so just convert {0, 0, 0} to world space.

// Run this in a detail wrangle
string cam = chsop("cam");
vector camPos = fromNDC(cam, {0, 0, 0}); // or {0, 0, 0} * optransform(cam);
addpoint(0, camPos);
{0.5, 0.5, 0} is technically more correct, but gives the same result.
Draw a ray from the camera
The Z axis aligns with the camera direction, so move along it to draw a ray.
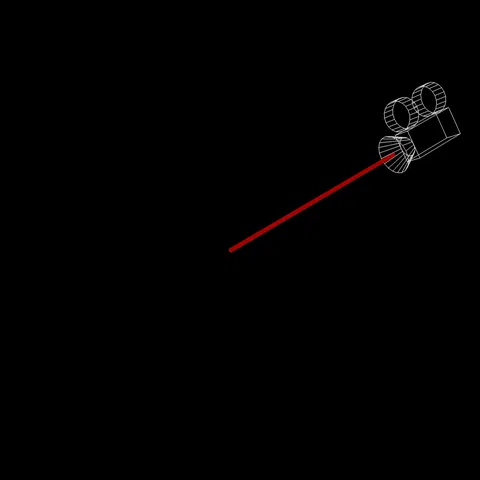
// Run this in a detail wrangle
string cam = chsop("cam");
float offset = chf("raylength");
// Sample two positions along the Z axis in NDC space to draw a ray
vector camPos = fromNDC(cam, {0.5, 0.5, 0});
vector camPos2 = fromNDC(cam, set(0.5, 0.5, -offset));
int a = addpoint(0, camPos);
int b = addpoint(0, camPos2);
addprim(0, "polyline", a, b);
Flatten to the XY plane
Using NDC coordinates directly in world space flattens the geometry to how it looks on screen, like a printed photo.

string cam = chsop("cam");
// Flatten by setting Z to a constant value
v@P = toNDC(cam, v@P);
v@P.z = 0;
Another trick is turning this into an outline, much like Labs Extract Silouette.
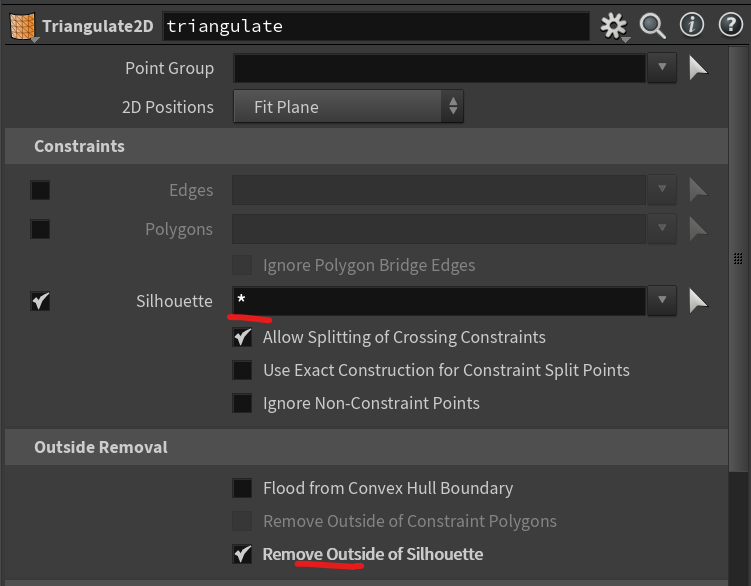
- Add a Triangulate2D node. Set “Silhouette” to
*and enable outside removal. This triangulates the mesh.
 |
 |
- Add a Divide node set to “Remove Shared Edges”. This wipes the interior triangles and produces a clean outline.
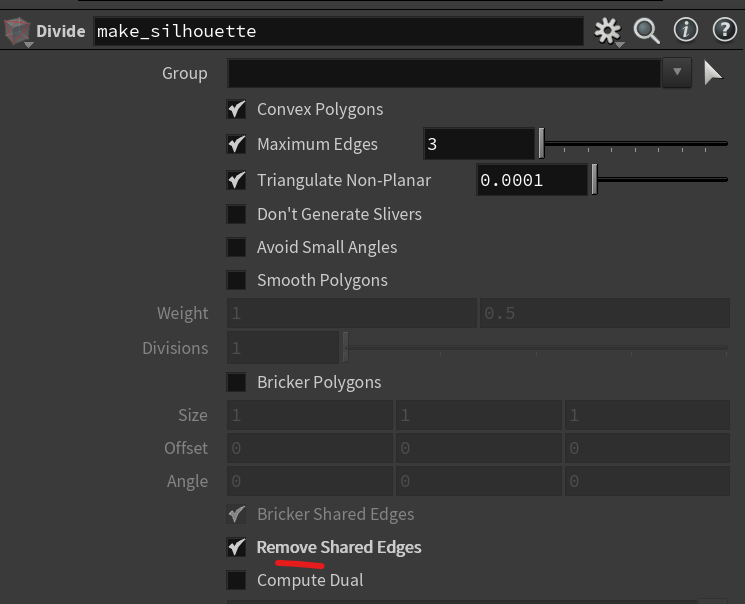 |
 |
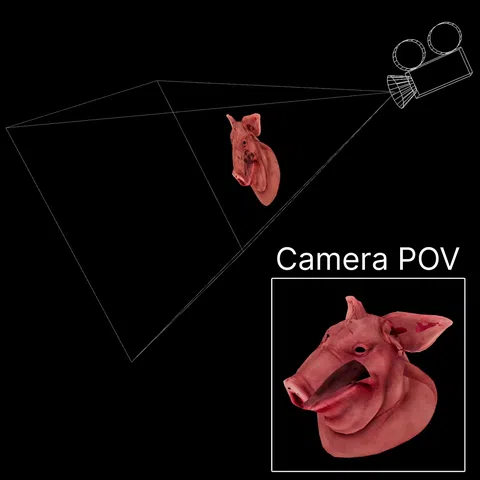
Flatten to the camera plane
Using NDC coordinates in camera space lets you flatten geometry but keep it identical from the camera perspective.
string cam = chsop("cam");
float offset = ch("distance");
// Flatten to camera by setting Z to a constant value
vector p = toNDC(cam, v@P);
p.z = -offset;
v@P = fromNDC(cam, p);
Move along the Z axis
Same as above, except subtracting the Z coordinate. Again the geometry is identical from the camera perspective.

string cam = chsop("cam");
float offset = ch("distance");
// Distort relative to camera by adding or multiplying the Z value
vector p = toNDC(cam, v@P);
p.z -= offset;
v@P = fromNDC(cam, p);
Perspective illusion
Same as above, except using another camera as reference. The Z coordinates are flipped as the cameras cross paths.

string cam = chsop("cam");
float mult = ch("multiply");
float add = ch("add");
// Distort relative to camera by adding or multiplying the Z value
vector p = toNDC(cam, v@P);
p.z = p.z * mult + add;
v@P = fromNDC(cam, p);
Frustum box
The VEX equivalent of Camera Frustum qL.
- Add a box. The X and Y coordinates range from 0 to 1. The Z coordinates are negative from 0 to the depth you want.
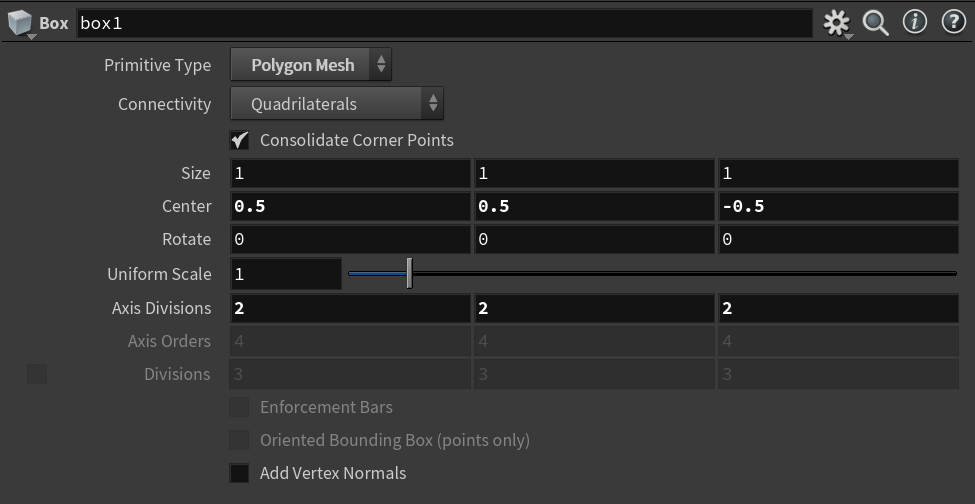 |
 |
- Convert from NDC to world coordinates.
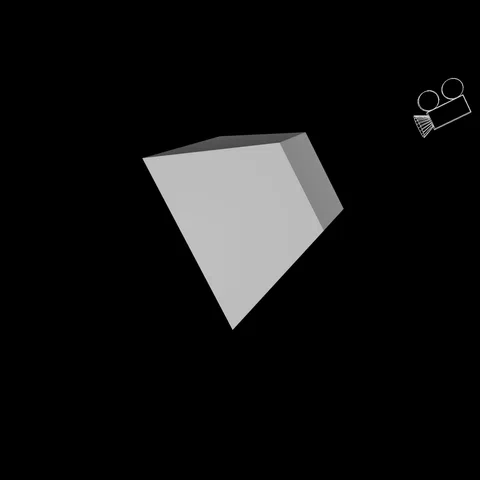
string cam = chsop("cam");
// Optionally animate it along the Z axis
v@P.z -= chf("distance");
v@P = fromNDC(cam, v@P);
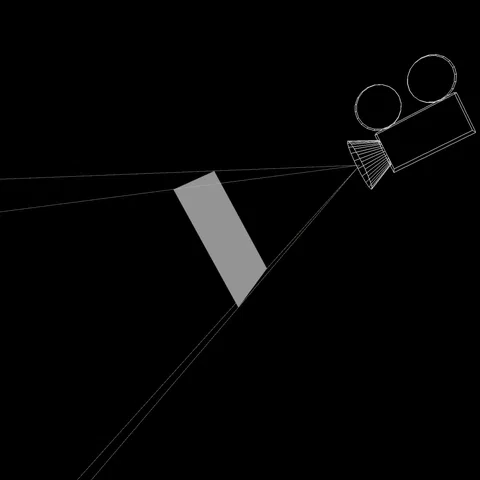
Frustum plane
The VEX equivalent of Camera Plane qL.
- Same as above, but add a grid instead. The X and Y coordinates range from 0 to 1.
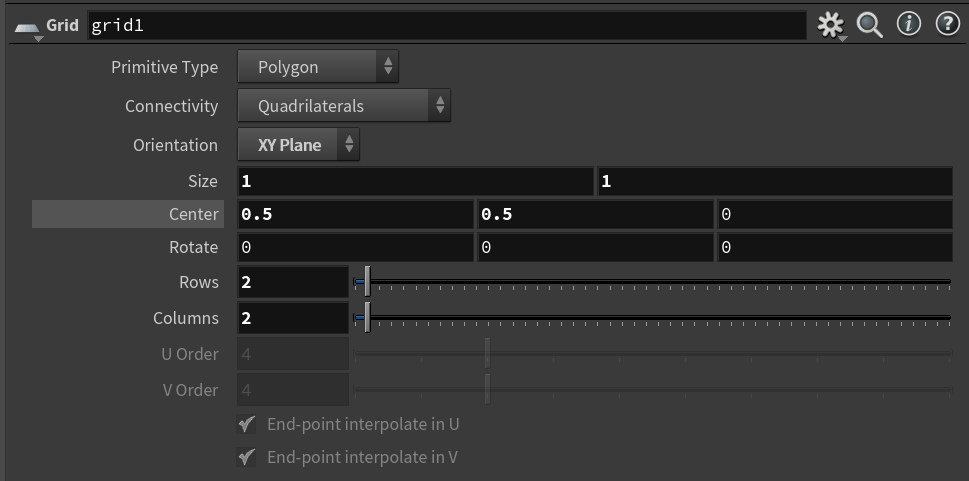 |
 |
- Convert from NDC to world coordinates.
string cam = chsop("cam");
// Optionally animate it along the Z axis
v@P.z = -chf("distance");
v@P = fromNDC(cam, v@P);
Project onto geometry
This technique is great for holograms. I first saw Entagma use it for a raytracer.
- Take the frustum plane above and subdivide it a bunch.
- Find the projection direction per point.
Since the plane is flattened on Z in NDC space, this is easy. Just subtract the camera position from the current position.
string cam = chsop("cam");
vector camPos = fromNDC(cam, {0, 0, 0});
// Projection direction
v@N = normalize(v@P - camPos);
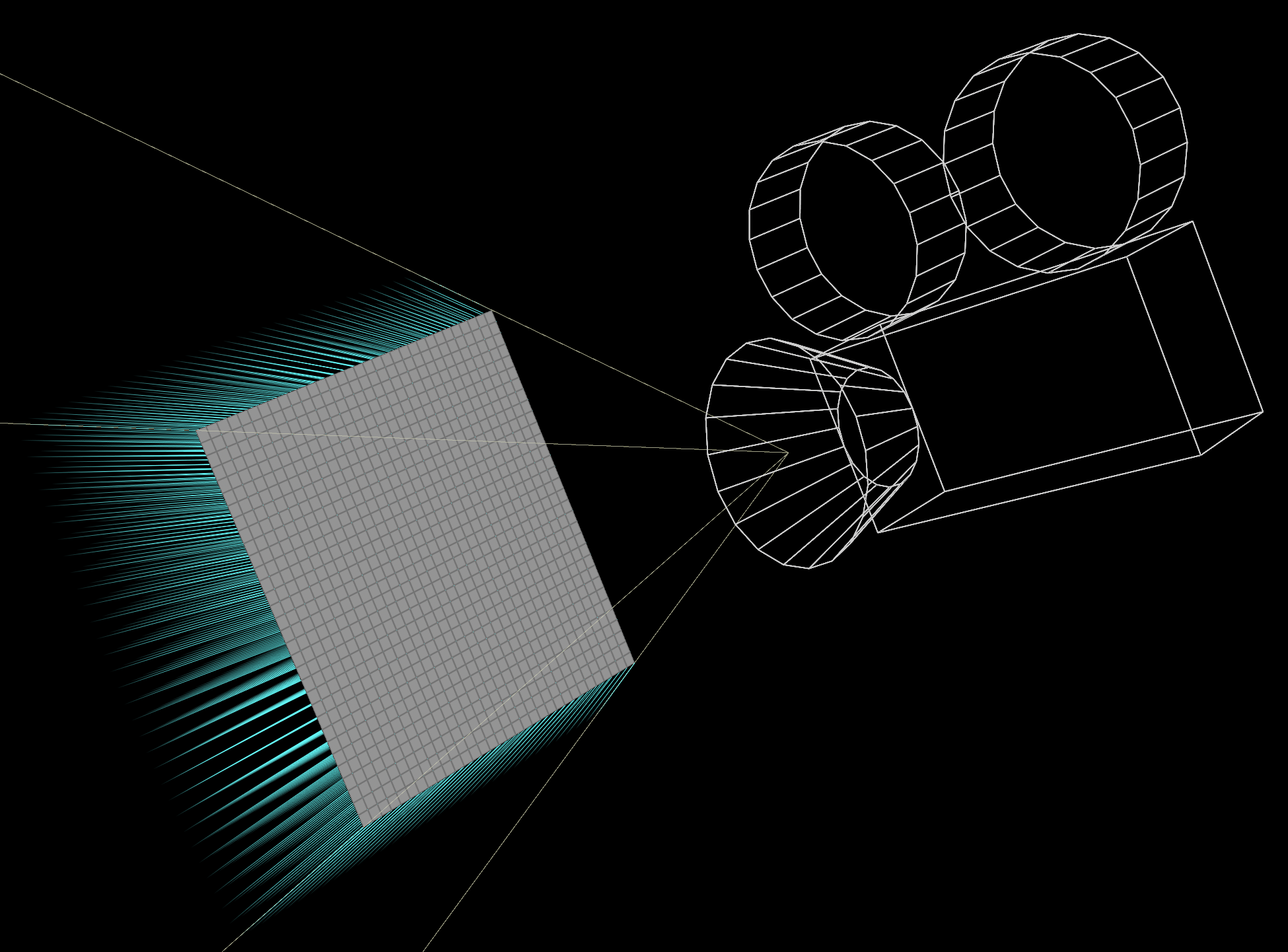
- Ray onto the target geometry.

For arbitrary geometry, the same idea applies. Convert to NDC space, flatten Z and convert back to world space.
string cam = chsop("cam");
vector camPos = fromNDC(cam, {0, 0, 0});
// Flatten Z axis in NDC space
vector ndcPos = toNDC(cam, v@P);
ndcPos.z = -1;
vector worldPos = fromNDC(cam, ndcPos);
// Projection direction
v@N = normalize(worldPos - camPos);
Project depth maps
Assuming no distortion, depth maps are easy to project using NDC coordinates.
You can get a depth map from Copernicus using Rasterize Geometry with intrinsic:depth_eye.

To project into world space, just set the Z coordinate to the color of the texture. @depth came from Attribute From Map.

string cam = chsop("cam");
v@P.z = -f@depth - chf("offset");
v@P = fromNDC(cam, v@P);
Cull offscreen geometry
Perhaps the most common use of NDC space is removing offscreen geometry.
So what is offscreen? For X and Y it’s anything outside the 0 to 1 range, and for Z it’s anything positive.

string cam = chsop("cam");
vector ndcPos = toNDC(cam, v@P);
if (ndcPos.x < 0 || ndcPos.x > 1 // Remove outside 0-1 on X
|| ndcPos.y < 0 || ndcPos.y > 1 // Remove outside 0-1 on Y
|| ndcPos.z >= 0) { // Remove behind camera (positive Z)
removepoint(0, i@ptnum);
}
It helps to add some wiggle room near the edges to avoid issues like glitchy motion blur or flickering shadows.

float padding = chf("padding");
string cam = chsop("cam");
vector ndcPos = toNDC(cam, v@P);
if (ndcPos.x < -padding || ndcPos.x > 1 + padding // Remove outside 0-1 on X (with padding)
|| ndcPos.y < -padding || ndcPos.y > 1 + padding // Remove outside 0-1 on Y (with padding)
|| ndcPos.z >= 0) { // Remove behind camera (positive Z)
removepoint(0, i@ptnum);
}
Cull geometry facing away from camera
You can measure the correlation between the camera direction and object normal using dot(v@N, camDir).
Using this as the Clip attribute, you clear any geometry facing away from the camera.

string cam = chsop("cam");
// dot() finds correlation between the normal direction and camera direction
vector camPos = fromNDC(cam, {0, 0, 0});
vector camDir = normalize(camPos - v@P);
// Use this attribute with Clip
f@correlation = dot(v@N, camDir);
Cull occluded geometry
You can remove occluded geometry by raying towards the camera to see if any collisions occur.
If no hit occurs, it must be visible to the camera. Otherwise it’s occluded and can be removed.
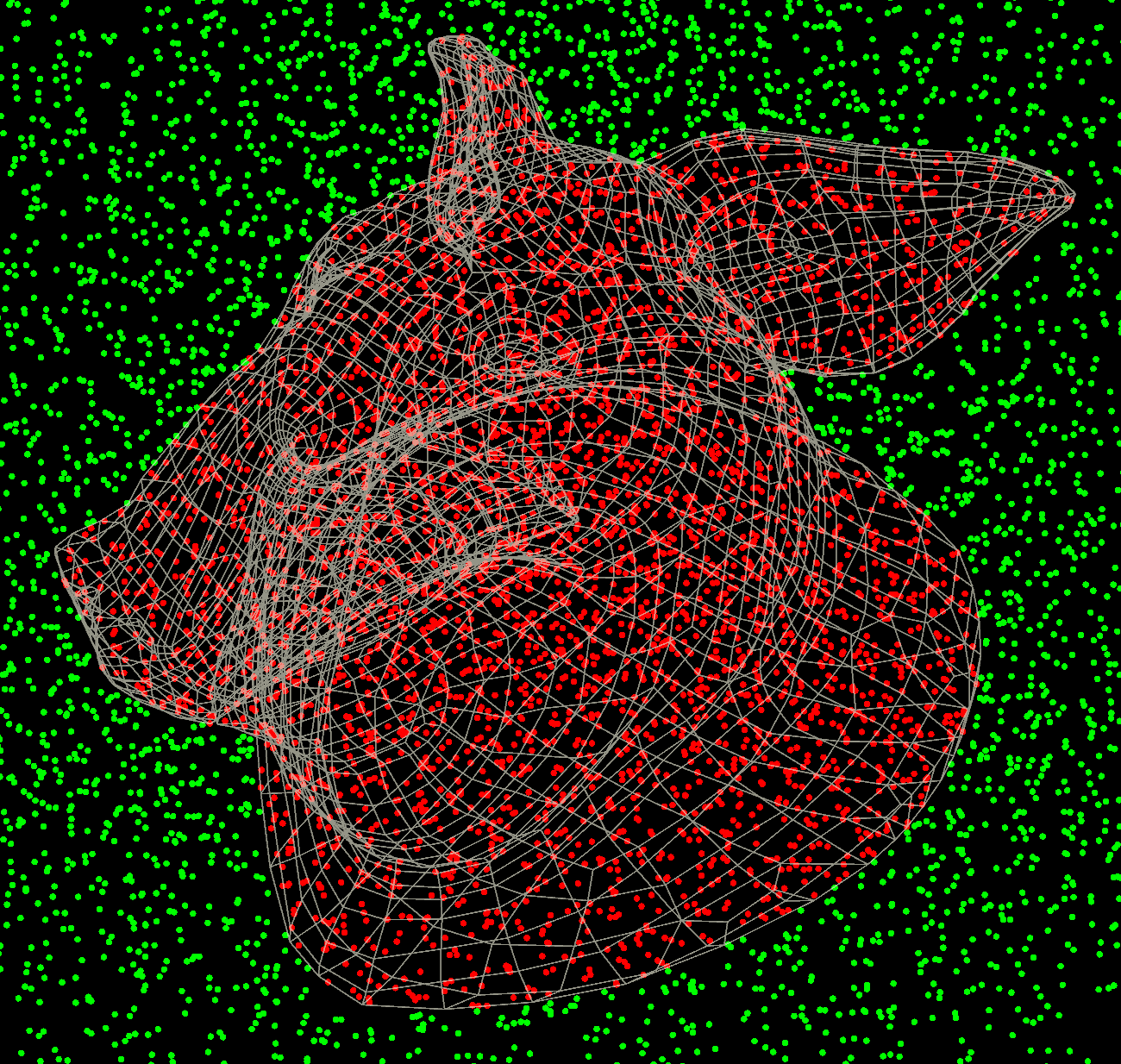
string cam = chsop("cam");
vector camPos = fromNDC(cam, {0, 0, 0});
vector camDir = camPos - v@P;
// Ray towards the camera and see if we hit the 2nd input
vector p, uvw;
if (intersect(1, v@P, camDir, p, uvw) >= 0) {
removepoint(0, i@ptnum);
}
Build your own NDC matrix
You can use perspective() to build a matrix that has the same effect as toNDC() (assuming the camera is in perspective mode).
Thanks to Igor Elovikov for sharing the code below! He noted this:
VEX
toNDC()feels a bit misleading and confusing.
Usually NDC space is a cube from (-1, 1, 1) to (1, 1, 1), but VEX transforms it to screen space and removes normalization from Z.
So X, Y is normalized but Z is the actual Z, the distance from the camera.
Also when you’re doing stuff manually, you should work with homogenous coordinates (vector4 basically).
string cam = chsop("cam");
4@projection = perspective(
chf(cam + "/focal") / chf(cam + "/aperture"),
chf(cam + "/resx") / chf(cam + "/resy"),
chf(cam + "/aspect"),
0, 1,
{-1, -1, 1, 1}
);
4@world_to_camera = invert(optransform(cam)); // or getspace("space:world", cam);
4@to_ndc = 4@world_to_camera * 4@projection;
// Equivalent to v@P = toNDC(cam, v@P);
vector4 pos = vector4(v@P) * 4@to_ndc;
v@P = vector(pos) / pos.w;
v@P.z = pos.z;
Try this version if you want Z to be normalized:
string cam = chsop("cam");
4@projection = perspective(
chf(cam + "/focal") / chf(cam + "/aperture"),
chf(cam + "/resx") / chf(cam + "/resy"),
chf(cam + "/aspect"),
chf(cam + "/near"),
chf(cam + "/far")
);
4@world_to_camera = invert(optransform(cam)); // or getspace("space:world", cam);
4@to_ndc = 4@world_to_camera * 4@projection;
v@P *= 4@to_ndc;
Convert both ways
Igor also shared how to calculate fromNDC() based on a modified version of toNDC().
Inverse transform is tricky as it involves the inversion of what I did before (denormalization of Z)
Also you have to keep the W component of the point
Actually I saw somewhere there should be an implicit 4th component, but not sure.
toNDC()
string cam = chsop("cam");
f@near = chf(cam + "/near");
f@far = chf(cam + "/far");
4@projection = perspective(
chf(cam + "/focal") / chf(cam + "/aperture"),
chf(cam + "/resx") / chf(cam + "/resy"),
chf(cam + "/aspect"),
f@near,
f@far,
{-1, -1, 1, 1}
);
4@world_to_camera = invert(optransform(cam)); // or getspace("space:world", cam);
4@to_ndc = 4@world_to_camera * 4@projection;
float clip_z = f@far - f@near;
// Equivalent to v@P = toNDC(cam, v@P);
vector4 pos = vector4(v@P) * 4@to_ndc;
v@P = vector(pos) / pos.w;
v@P.z = f@near + pos.z * clip_z;
f@origin_w = pos.w;
fromNDC()
vector4 pos = v@P;
pos.z = invlerp(v@P.z, f@near, f@far) / f@origin_w;
pos *= invert(4@to_ndc);
v@P = vector(pos) / pos.w;